Instrumental variable analysis with a binary outcome

8 minute read

Here is an additional post on instrumental variable (IV) analysis. This follows an exercise where I employed two methods of IV analysis, comparing a Bayesian approach with two-stage least squares (2SLS). My motivation for these posts is to have a better understanding, ultimately, of Mendelian randomization. The context in which I ultimately want to apply it to is a disease outcome, which is binary. In this post, I explore the Bayesian approach of IV analysis towards a binary outcome.

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import scipy.stats as stats
import seaborn as sns
from scipy.special import expit
from utils import draw_causal_graph, standardize

RANDOM_SEED = 73
np.random.seed(RANDOM_SEED)
sns.set_context("talk")
sns.set_palette("colorblind")
cb_palette = sns.color_palette()

Notes

  • check p per subject
  • model, binary outcome, variable n

Causal graph of example dataset with binary outcome

We’ll return to the wages and education example from Chapter 14 of Statistical Rethinking. However, instead of using wages as our outcome, we’ll tweak this by creating a binary outcome from wages, which I’ll refer to as $R$ for “rich”. The causal diagram will look the same as a traditional IV setup.

draw_causal_graph(
    edge_list=[("Q", "E"), ("U", "E"), ("U", "R"), ("E", "R")],
    node_props={"U": {"style": "dashed"}},
    graph_direction="TD",
)

svg

Per usual, we’ll use this to generate a simulated dataset. We’ll use the same code but this time derive R from W. The rationale being those with higher wages are more likely to be rich. We’ll still making the influence of education on wages (bEW_sim) equal to 0. We’ll want to get this value back in our statistical models, even though we’ll be using R as our ultimate outcome variable.

A key conceptual point is use of a logit link function to produce R from W. Additionally, we’ll make use of a binomial generalized linear model.

def generate_data(num_subjects, n_binomial_param) -> pd.DataFrame:
    """Generate simulated data.

    Parameters
    ----------
    num_subjects
        Number of subjects/rows in data
    n_binomial_param
        Number of "observations" for each subject;
        a parameter in the binomial GLM

    Returns
    -------
    sim_df
        pd.DataFrame

    """

    bEW_sim = 0

    U_sim = np.random.normal(size=num_subjects)
    Q_sim = np.random.randint(1, 5, size=num_subjects)
    E_sim = np.random.normal(loc=U_sim + Q_sim, size=num_subjects)
    W_sim = np.random.normal(loc=U_sim + bEW_sim * E_sim, size=num_subjects)
    sim_df = pd.DataFrame.from_dict(
        {"W": standardize(W_sim), "E": standardize(E_sim), "Q": standardize(Q_sim)}
    )

    # Use of link functions to generate R
    index_val = sim_df.index.values
    sim_df["R"] = stats.binom.rvs(n=n_binomial_param, p=expit(W_sim))
    sim_df["R_size"] = n_binomial_param

    return sim_df


dat_sim = generate_data(num_subjects=500, n_binomial_param=2)
dat_sim.head()
W E Q R R_size
0 -1.327032 -0.600469 0.453638 1 2
1 -0.108554 -0.159673 -1.318387 0 2
2 -0.908108 1.066808 0.453638 2 2
3 -2.187143 -2.856829 -1.318387 0 2
4 0.044873 -0.024763 -0.432374 1 2

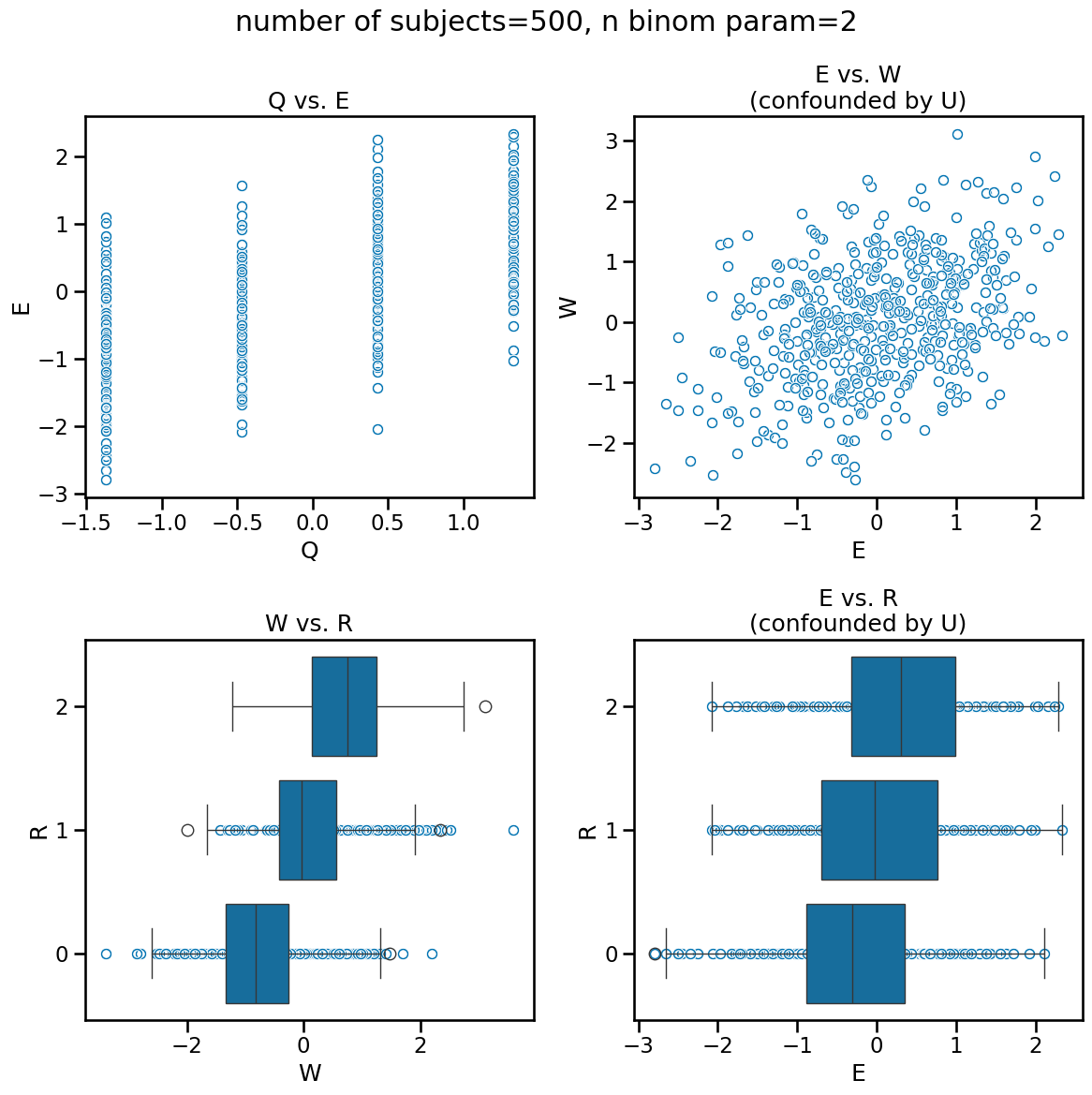
As usual, visualizing the data can give us some insight into how the data appears and where confounds may mislead. We know that Q is a cause of E and therefore the association we see is reflective of causation. The bottom-left figure W vs. R is a logit transformation of the former into the latter. However, both the plots in the right column are a result of the confound U. It is driving the relationship between E and W and therefore we also see an association between E and R.

def plot_variable_relationships(sim_df, title):
    f, ((ax0, ax1), (ax2, ax3)) = plt.subplots(2, 2, figsize=(12, 12))

    sns.scatterplot(data=sim_df, x="Q", y="E", marker=r"$\circ$", ax=ax0)
    ax0.set_title("Q vs. E")

    sns.scatterplot(data=sim_df, x="E", y="W", marker=r"$\circ$", ax=ax1)
    ax1.set_title("E vs. W\n(confounded by U)")

    sns.boxplot(data=sim_df, x="W", y="R", orient="h", color=cb_palette[0], ax=ax2)
    sns.scatterplot(data=dat_sim_n1, x="W", y="R", marker=r"$\circ$", ax=ax2)
    ax2.invert_yaxis()
    ax2.set_title("W vs. R")

    sns.boxplot(data=sim_df, x="E", y="R", orient="h", color=cb_palette[0], ax=ax3)
    sns.scatterplot(data=sim_df, x="E", y="R", marker=r"$\circ$", ax=ax3)
    ax3.invert_yaxis()
    ax3.set_title("E vs. R\n(confounded by U)")

    f.suptitle(title)
    f.tight_layout()


plot_variable_relationships(dat_sim, "number of subjects=500, n binom param=2")

png

Bayesian model with binary outcome

We’ll use the Bayesian approach to run our inferential model. Again, the important thing is the link function to get our count output.

\[R_i \sim \text{Binomial}(n_i, p_i)\] \[\text{logit}(p_i) = W_i\] \[\left( \begin{array}{c} W_i \\ {E_i} \end{array} \right) \sim \text{MVNormal} \left( \begin{array}{c}{\mu_{W_i}} \\ {\mu_{E_i} } \end{array} , \textbf{S} \right)\] \[\mu_{W_i} = \alpha_W + \beta_{EW} W_i\] \[\mu_{E_i} = \alpha_E + \beta_{QE} E_i\] \[\alpha_W, \alpha_E \sim \text{Normal}(0, 0.2)\] \[\beta_{EW}, \beta_{QE} \sim \text{Normal}(0, 1.5)\] \[\textbf{S} = \begin{pmatrix} \sigma_{W}^2 & \rho\sigma_{W}\sigma_{E} \\ \rho\sigma_{W}\sigma_{E} & \sigma_{E}^2 \end{pmatrix} = \begin{pmatrix} \sigma_{P} & 0 \\ 0 & \sigma_{\beta} \end{pmatrix} \textbf{R} \begin{pmatrix} \sigma_{W} & 0 \\ 0 & \sigma_{E} \end{pmatrix}\] \[\textbf{R} \sim \text{LKJCorr}(2)\] 
def run_bayesian_iv_model_binary(data_df):
    """Model for education/rich binary outcome.

    Parameters
    ----------
    data_df
        Generated dataset

    Returns
    -------
    :
        pymc idata object
    """

    index_vals = data_df.index.values

    with pm.Model() as model:
        aW = pm.Normal("aW", 0.0, 0.2)
        aE = pm.Normal("aE", 0.0, 0.2)
        bEW = pm.Normal("bEW", 0.0, 0.5)
        bQE = pm.Normal("bQE", 0.0, 0.5)

        muW = pm.Deterministic("muW", aW + bEW * data_df.E.values)
        muE = pm.Deterministic("muE", aE + bQE * data_df.Q.values)

        chol, _, _ = pm.LKJCholeskyCov(
            "chol_cov", n=2, eta=2, sd_dist=pm.Exponential.dist(1.0), compute_corr=True
        )

        # multivariate regression
        MU = pt.stack([muW, muE]).T
        YY_obs = pm.Data("YY_obs", data_df[["R", "E"]].values)
        YY = pm.MvNormal("YY", mu=MU, chol=chol, observed=YY_obs)

        # link function
        p = pm.Deterministic("p", pm.math.invlogit(YY[index_vals, 0]))
        R = pm.Binomial("R", n=data_df["R_size"], p=p, observed=data_df["R"])

        idata = pm.sample(1000, random_seed=RANDOM_SEED, target_accept=0.95)
        idata.rename({"chol_cov_corr": "Rho", "chol_cov_stds": "Sigma"}, inplace=True)

    return idata

idata_14_6_logit = run_bayesian_iv_model_binary(dat_sim)

Sampling 4 chains, 0 divergences ━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━  32% 0:00:17 / 0:00:10

IOPub message rate exceeded.
The Jupyter server will temporarily stop sending output
to the client in order to avoid crashing it.
To change this limit, set the config variable
`--ServerApp.iopub_msg_rate_limit`.

Current values:
ServerApp.iopub_msg_rate_limit=1000.0 (msgs/sec)
ServerApp.rate_limit_window=3.0 (secs)

IOPub message rate exceeded.
The Jupyter server will temporarily stop sending output
to the client in order to avoid crashing it.
To change this limit, set the config variable
`--ServerApp.iopub_msg_rate_limit`.

Current values:
ServerApp.iopub_msg_rate_limit=1000.0 (msgs/sec)
ServerApp.rate_limit_window=3.0 (secs)

IOPub message rate exceeded.
The Jupyter server will temporarily stop sending output
to the client in order to avoid crashing it.
To change this limit, set the config variable
`--ServerApp.iopub_msg_rate_limit`.

Current values:
ServerApp.iopub_msg_rate_limit=1000.0 (msgs/sec)
ServerApp.rate_limit_window=3.0 (secs)

IOPub message rate exceeded.
The Jupyter server will temporarily stop sending output
to the client in order to avoid crashing it.
To change this limit, set the config variable
`--ServerApp.iopub_msg_rate_limit`.

Current values:
ServerApp.iopub_msg_rate_limit=1000.0 (msgs/sec)
ServerApp.rate_limit_window=3.0 (secs)







Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 48 seconds.




f, ax0 = plt.subplots(1, 1, figsize=(6, 5), sharex=True)
az.plot_forest(idata_14_6_logit, var_names=["bEW", "bQE"], combined=True, ax=ax0)
ax0.set_title("m14.6 with logistic link")




Text(0.5, 1.0, 'm14.6 with logistic link')




png



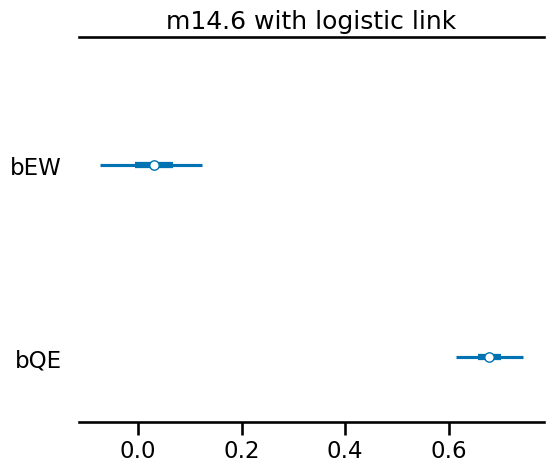
As you can see, we get coefficients as the original wages and education example.



Experimenting with number of subjects and the binomial parameter



A practical question we might have in a real world scenario is how many subjects we might need and how many observations we might want per person. Generally, more people will give us more power for our estimate. We can run experiments to help us understand how these parameters influence the credible interval of our estimate.



num_subjects_list = [25, 100, 200, 500]
n_binomial_param_list = [1, 2, 5]




def format_summary_table(
    idata, num_subjects, n_binomial_param, var_names=["bEW", "bQE"]
):
    df = (
        az.summary(idata, var_names=var_names)
        .assign(num_subjects=num_subjects)
        .assign(n_binomial_param=n_binomial_param)
    )
    return df




df_summary = list()
for num_subjects in num_subjects_list:
    for n_binomial_param in n_binomial_param_list:
        print(
            f"Running {num_subjects} num_subjects, {n_binomial_param} n_binomial_param..."
        )
        dat_sim_expt = generate_data(
            num_subjects=num_subjects, n_binomial_param=n_binomial_param
        )
        idata_14_6_logit_expt = run_bayesian_iv_model_binary(dat_sim_expt)
        df_expt_summary = format_summary_table(
            idata_14_6_logit_expt,
            num_subjects=num_subjects,
            n_binomial_param=n_binomial_param,
        )
        df_summary.append(df_expt_summary)

print("Done with experiment")
df_summary = pd.concat(df_summary)
df_summary








  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
      mcse_mean
      mcse_sd
      ess_bulk
      ess_tail
      r_hat
      num_subjects
      n_binomial_param
    

  
  
    

      bEW
      0.254
      0.163
      -0.067
      0.556
      0.005
      0.003
      1330.0
      1345.0
      1.0
      25
      1
    

    

      bQE
      0.430
      0.174
      0.087
      0.741
      0.003
      0.002
      3144.0
      2492.0
      1.0
      25
      1
    

    

      bEW
      0.075
      0.290
      -0.491
      0.606
      0.007
      0.005
      1558.0
      1779.0
      1.0
      25
      2
    

    

      bQE
      0.572
      0.158
      0.256
      0.841
      0.003
      0.002
      2945.0
      2536.0
      1.0
      25
      2
    

    

      bEW
      -0.118
      0.447
      -1.018
      0.664
      0.009
      0.007
      2226.0
      2858.0
      1.0
      25
      5
    

    

      bQE
      0.503
      0.153
      0.203
      0.777
      0.003
      0.002
      2942.0
      2430.0
      1.0
      25
      5
    

    

      bEW
      0.069
      0.077
      -0.078
      0.212
      0.002
      0.001
      2062.0
      1784.0
      1.0
      100
      1
    

    

      bQE
      0.631
      0.078
      0.491
      0.780
      0.001
      0.001
      4154.0
      3071.0
      1.0
      100
      1
    

    

      bEW
      0.097
      0.134
      -0.157
      0.339
      0.003
      0.002
      1835.0
      1786.0
      1.0
      100
      2
    

    

      bQE
      0.589
      0.079
      0.442
      0.736
      0.001
      0.001
      2903.0
      2622.0
      1.0
      100
      2
    

    

      bEW
      -0.723
      0.394
      -1.434
      0.028
      0.012
      0.009
      1025.0
      1450.0
      1.0
      100
      5
    

    

      bQE
      0.555
      0.087
      0.389
      0.718
      0.002
      0.002
      1328.0
      2054.0
      1.0
      100
      5
    

    

      bEW
      -0.026
      0.055
      -0.129
      0.077
      0.001
      0.001
      2076.0
      2150.0
      1.0
      200
      1
    

    

      bQE
      0.637
      0.055
      0.533
      0.738
      0.001
      0.001
      3645.0
      2818.0
      1.0
      200
      1
    

    

      bEW
      0.241
      0.086
      0.083
      0.405
      0.002
      0.001
      2431.0
      2040.0
      1.0
      200
      2
    

    

      bQE
      0.607
      0.055
      0.509
      0.715
      0.001
      0.001
      3814.0
      2899.0
      1.0
      200
      2
    

    

      bEW
      -0.232
      0.233
      -0.659
      0.200
      0.007
      0.005
      1234.0
      1331.0
      1.0
      200
      5
    

    

      bQE
      0.589
      0.060
      0.479
      0.704
      0.001
      0.001
      1758.0
      2294.0
      1.0
      200
      5
    

    

      bEW
      -0.013
      0.035
      -0.077
      0.054
      0.001
      0.001
      2187.0
      2619.0
      1.0
      500
      1
    

    

      bQE
      0.640
      0.034
      0.581
      0.707
      0.001
      0.000
      3164.0
      3009.0
      1.0
      500
      1
    

    

      bEW
      0.109
      0.057
      -0.001
      0.212
      0.001
      0.001
      2186.0
      2422.0
      1.0
      500
      2
    

    

      bQE
      0.617
      0.035
      0.548
      0.682
      0.001
      0.000
      3594.0
      2525.0
      1.0
      500
      2
    

    

      bEW
      0.026
      0.120
      -0.202
      0.240
      0.003
      0.002
      1838.0
      2026.0
      1.0
      500
      5
    

    

      bQE
      0.605
      0.036
      0.538
      0.673
      0.001
      0.001
      2578.0
      2687.0
      1.0
      500
      5
    

  






Results of experiments with generated data parameters



f, (ax0, ax1) = plt.subplots(1, 2, figsize=(12, 5), sharey=True)

def plot_mean_and_ci(coefficient, ax):
    x_shifts = [-15, 0, 15]
    n_binomial_param_list = [1, 2, 5]
    colors = cb_palette[0:3]
    for n_binom, x_shift, color in zip(n_binomial_param_list, x_shifts, colors):
        df = (
            df_summary.reset_index(names="coefficient")
            .query("coefficient==@coefficient")
            .query("n_binomial_param==@n_binom")
        )
        ax.scatter(df["num_subjects"]+x_shift, df["mean"], facecolors=None, edgecolor=color, s=2**4, label=n_binom)
        ax.vlines(x=df["num_subjects"]+x_shift, ymin=df["hdi_3%"], ymax=df["hdi_97%"], linewidth=0.75, color=color)
    ax.set_title(coefficient)
    ax.set(
        xlabel="Number of subjects",
        ylabel="Estimate"
        
    )
    if coefficient == "bQE":    
        ax.legend(title='n_binomial_param', title_fontsize=12, fontsize=12, loc='lower right')

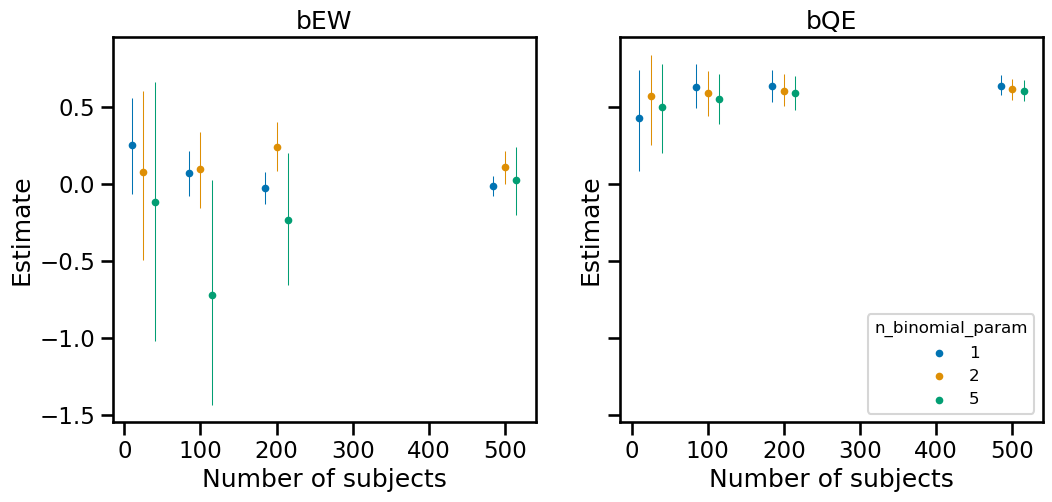
plot_mean_and_ci("bEW", ax0)
plot_mean_and_ci("bQE", ax1)





png



g = sns.relplot(
    data=df_summary.reset_index(names="coefficient"),
    x="num_subjects",
    y="sd",
    hue="n_binomial_param",
    hue_order = [1,2,5],
    col="coefficient",
    palette=cb_palette[0:3],
    kind='line'
)

g.set_titles(col_template="{col_name}")
g.set_axis_labels(x_var="Number of subjects", y_var="SD of coefficient")
plt.setp(g._legend.get_texts(), fontsize='12')
plt.setp(g._legend.get_title(), fontsize='12');




png



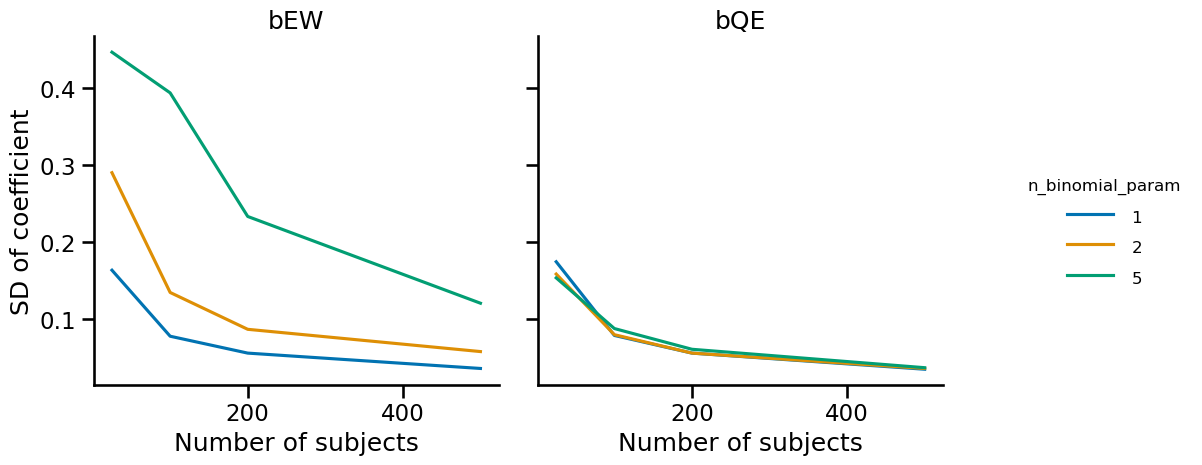
First, it makes sense that the variability of bQE is not affected by the binomial parameter since this coefficient is not dependent on the logit transformation. The variability of the bEW decreases with the number of subjects, as one might intuit. But I didn’t necessarily expect that a higher $n$ as a binomial parameter would lead to higher variability.



Summary and acknowledgements



My motivation for this post was understanding how to implement IV analysis with a binary outcome. I also ran an experiment to determine appropriate sample sizes. Some of the coding implementation was tricky for me initially. Thanks to the man himself for providing some help.



%load_ext watermark
%watermark -n -u -v -iv -w




The watermark extension is already loaded. To reload it, use:
  %reload_ext watermark
Last updated: Wed Jun 12 2024

Python implementation: CPython
Python version       : 3.12.3
IPython version      : 8.24.0

pymc      : 5.15.0
matplotlib: 3.8.4
scipy     : 1.13.0
seaborn   : 0.13.2
numpy     : 1.26.4
pandas    : 2.2.2
arviz     : 0.18.0
pytensor  : 2.20.0

Watermark: 2.4.3




        
      


      

      


      
  

    


    
  


  
  
    

      
You May Also Enjoy

      

        
          





  



        
          





  

    
    

      
        Time series with varying intercepts

      
    

    

  

    

    

    
      
      

      
        
        
          10 minute read
        
      
    
  



    
I’ve done time-series data with time-to-event models and would like to explore modeling with mixed effects models. I’ll take an interative approach, in the s...

  




        
          





  

    
    

      
        Follow-up after getting causal estimates

      
    

    

  

    

    

    
      
      

      
        
        
          1 minute read
        
      
    
  



    
Notes for Chapter 5 of Causal Inference with Survey Data on LinkedIn Learning, given by Franz Buscha. I’m using this series of posts to take some notes.



  




        
          





  

    
    

      
        Longitudinal Survey Designs

      
    

    

  

    

    

    
      
      

      
        
        
          7 minute read
        
      
    
  



    
Notes for Chapter 4 of Causal Inference with Survey Data on LinkedIn Learning, given by Franz Buscha. I’m using this series of posts to take some notes.